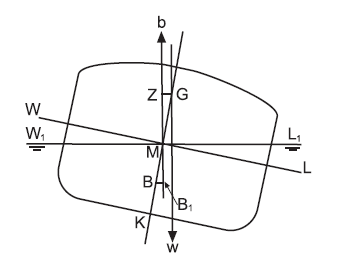
When a ship with negative initial metacentric height is inclined to a small angle, the righting lever is negative, resulting in a capsizing moment. This effect is shown in Figure and it can be seen that the ship will tend to heel still further.
At a large angle of heel the centre of buoyancy will have moved further out the low side and the force of buoyancy can no longer be considered to act vertically upwards though M, the initial metacentre.
To calculate the angle of loll
When the vessel is `wall-sided’ between the upright and inclined waterlines, the GZ may be found using the formula:
GZ = Sin Ө (GM + ½BM tan²Ө)
At the angle of loll:
GZ = 0
Therefore either sin Ө = 0
or
(GM + ½BM tan²Ө) = 0
If
sin Ө = 0
then
Ө = 0
But then angle of loll cannot be zero, therefore:
(GM + ½BM tan²Ө) = 0
½BM tan²Ө = – GM
BM tan²Ө= – 2GM
tan²Ө= – 2GM/BM
tanӨ= √-(2GM/BM)
The angle of loll is caused by a negative GM, therefore:
tanӨ= √-(-2GM/BM)
tanӨ= √(2GM/BM)
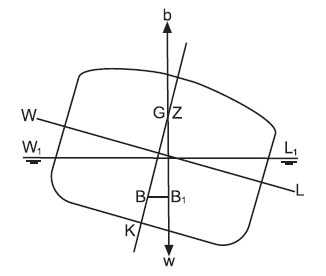
If, by heeling still further, the centre of buoyancy can move out far enough to lie vertically
under G the centre of gravity, as in Figure , the righting lever and thus the righting moment, will be zero.
The angle of heel at which this occurs is referred to as the angle of loll and may be defined as the angle to which a ship with negative initial metacentric height will lie at rest in still water.
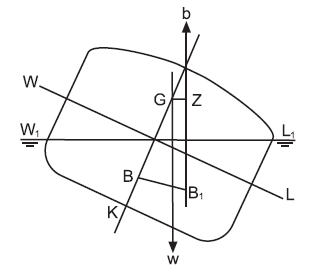
If the ship should now be inclined to an angle greater than the angle of loll, as shown in Figure, the righting lever will be positive, giving a moment to return the ship to the angle of loll.
From this it can be seen that the ship will oscillate about the angle of loll instead of the upright.
Curve of statical stability at Angle of Loll
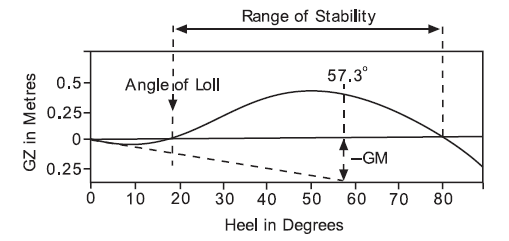
The curve of statical stability for a ship in this condition of loading is illustrated in Figure. Note from the figure that the GZ at the angle of loll is zero. At angles of heel less than the angle of loll the righting levers are negative, whilst beyond the angle of loll the righting levers are positive up to the angle of vanishing stability.
Note how the range of stability in this case is measured from the angle of loll and not from the `o±o’ axis.