Stability is the science of calculating the ability of ship to remain upright in all Conditions of weather and seas. One of the important aspects of determining such stability is the knowledge of areas and the volumes of the ship. Even though practical stability calculations do not require us to calculate these parameters at sea, it is necessary for us to understand the principles involved and to study the process of calculating the areas and volumes of various ship shapes.

Trapezoidal rules

A Trapezoid is a plane four-sided figure having two sides parallel. If the lengths of the parallel sides are Y1 and Y2 and they are “h” units apart then the area of trapezoid is given by A = h/2 (Y1+Y2) sq. units.

The trapezoidal rule assumes that the portion of the curve lying between any two consecutive ordinates Y1, Y2 etc. can be replaced with sufficient accuracy by a straight line. A curvilinear figure can be divided into a number of approximate trapezoids by covering it with N equally spaced vertical co-ordinates, ‘h’ units apart, the ordinates in order being Yl, Y2, Y3 etc.

The rule merely sums up all these separate trapezoids. The areas of the trapezoids are then:

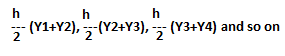
The total area of the figure is then given by

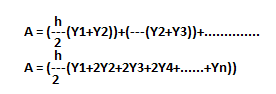
This can simplified further as:

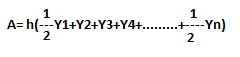
Remember the Definition of common interval “h” This is the distance between two successive ordinates. Remember the ordinates are evenly spaced by the common interval “h” throughout the length of the area. If the length of an area in question is 36 mtrs and it is divided into 12 equal parts then: (a) the total number of ordinates would be 13 (including the ends) (b) the number of common intervals would be 12. (c) “h” in this case would be 36/12 = 3 mtrs and not 36/13 = 2.769 mtrs.

Example

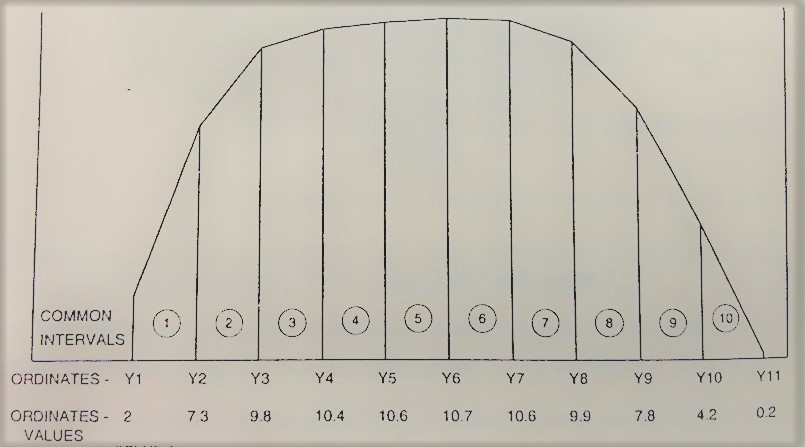
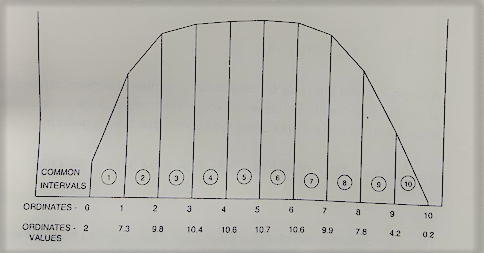
The half-breadths at equidistant stations of a ship’s waterplane of length 122 metres commencing from aft are as follows:

Station	0.	1.	2.	3.	4.	5.	6.	7.	8.	9.	10
Half Breadth	2.0	7.3	9.8	10.4	10.6	10.7	10.6	9.9	7.8	4.2	0.2

To determine total area of the water plane by the trapezoidal rule

Solution:

No of ordinate	½ breadth	Multiplier	Product of area
0	2.0	½	1.0
1	7.3	1	7.3
2	9.8	1	9.8
3	10.4	1	10.4
4	10.6	1	10.6
5	10.7	1	10.7
6	10.6	1	10.6
7	9.9	1	9.9
8	7.8	1	7.8
9	4.2	1	4.2
10	0.2	½	0.2
			Sum = 82.4

Common interval = h = 122/10 = 12.2 m

½ Area = h x sum = 12.2 x 82.4 = 1005.3 square metres

Total area = 2 x 1005.3 = 2010.6 square metres

Sirnpson’s first rule

Simpson’s first rule or three ordinate rule states that:

Area of the surface under a curve defined by an odd number of equally spaced ordinates Y1 , Y2, Y3 is given by:

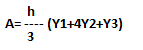
Area of the figure having 11 ordinates is found by compounding the multipliers as shown in the figure.

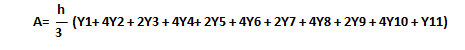
Example of Simpson’s first rule

Example:

The half-breadths at equidistant stations of a ship’s waterplane of length 122 metres commencing from aft are as follows

Solution :-

No of Ordinate	½ breadth	Simpson Multiplier	Product of area
0	2.0	1	2.0
1	7.3	4	29.2
2	9.8	2	19.6
3	10.4	4	41.6
4	10.6	2	21.2
5	10.7	4	42.8
6	10.6	2	21.2
7	9.9	4	39.6
8	7.8	2	15.6
9	4.2	4	16.8
10	0.2	1	0.2
			Sum = 249.8

Common interval = h = 122/10 = 12.2 m

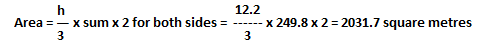
Simpson’s Second Rule

The rule was derived for four evenly spaced ordinates. It assumes the bounding curve to be a parabola of the third order. For four evenly spaced ordinates the rule is:

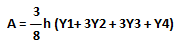
A long curvilinear area may be divided into a number of portions similar to the above to which the above rule would apply. The multipliers are compounded as shown in figure and the area under the curve in that case is given by

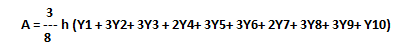
Example

The half ordinates if part of a ship’s waterplane are spaced 12m apart and are 4.2, 7.8, 9.98, 10.5, 10.6, 10.6, 10.4, 9.8, 7.3, 2.1 m respectively. Lets find out the total waterplane area by Simpson’s second rule

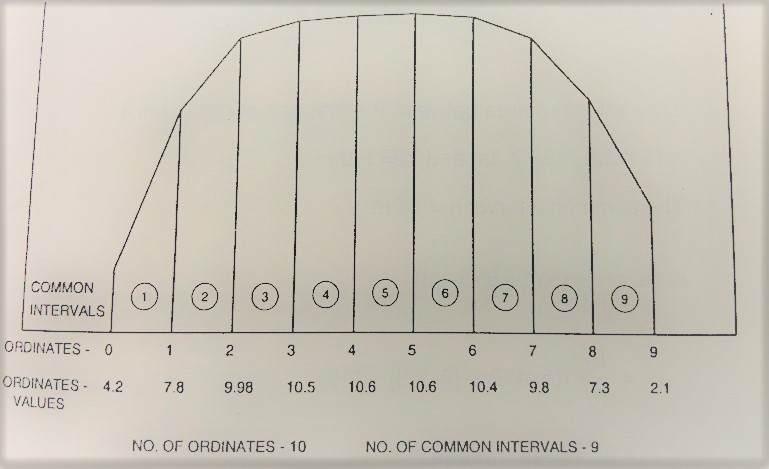
No of Ordinate	½ breadth	Multiplier	Product of area
0	4.2	1	4.2
1	7.8	3	23.4
2	9.98	3	29.7
3	10.5	2	21.0
4	10.6	3	31.8
5	10.6	3	31.8
6	10.4	2	20.8
7	9.8	3	29.4
8	7.3	3	21.9
9	2.1	1	2.1
			Sum=216.1

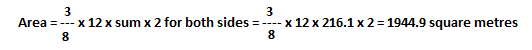
Simpson’s Third Rule (5, 8, -1 Rule)

This is useful rule, which gives the area between any two consecutive ordinates Y1 and Y2 when the next equispaced ordinate Y3 is also known. Y1 is known as the near ordinate and Y2 as middle ordinate and Y3 as the far ordinate

Area ABCF = h/12 (5Y1 + 8Y2 – Y3)

Area CDEF = h/12 (5Y3 8Y2 – Y3)

Example:

Determine the area between the first pair of ordinates if

Y1= 4.2m, Y2= 7.8m and Y3= 9.9 m

The common interval h = 14 m

Area = h/12 (5Y1 + 8Y2-Y3)

= 14/12 ((5×4.2) + (8×7.8) — 9.9)
= 86 square metres.

Simpson’s rules are nothing but an accurate version of the earlier mentioned trapezoid rule. Which rule to use ? The total number of ordinates (including the ends) determine which rule (1st , 2nd or 3rd rule) is to be used. Some times a combination of rules may have to be used depending on the number of ordinates.

No of Ordinates (including the ends)	Rule to Apply
3,5,7,9,11 and so on	1 (1 4 1 ) Rule
4,7,10,13,16 and so on	2 ( 1 3 3 1 ) Rule
3	3 (5 8- 1) rule. This rule will give the area under one pair or ordinates only depending on how you use it.

Any other number of ordinates

A combination of the above rules will have to be used. eg: if the number of ordinates are 6 then the rule 1 will be used to calculate the area between the 1,2,3 ordinates and rule 2 will be used to calculate the area between 3,4,5,6 ordinates. The total of both will give the area under the 1,2,3,4,5,6 ordinates. Remember the number of common intervals would be 5 as discussed earlier.