The sextant is an instrument used to measure angles. Its arc is one sixth of a circle. Hence it is called a sextant.
In actual practice, the arc of the sextant is about 60°. Being an instrument of double reflection, it can measure angles up to about 120°

Typically the sextant is used to measure the height of a celestial object above the observers visible horizon.

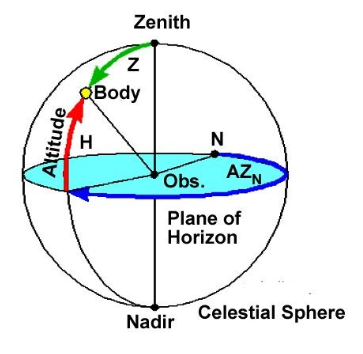
This angle is called the “the altitude of the celestial object” or simply “Altitude”. A marine sextant can measure angles with a precision of less than 0.5’ better than 1/100th of a degree.

Measurements by a sextant.

⦁ Altitudes of celestial bodies
⦁ A sextant is used to measure altitude of celestial body, vertical angles called vertical sextant angles (VSA) of terrestrial objects.
⦁ Horizontal angles called horizontal sextant angles (HSA) between terrestrial objects.

Construction of sextant

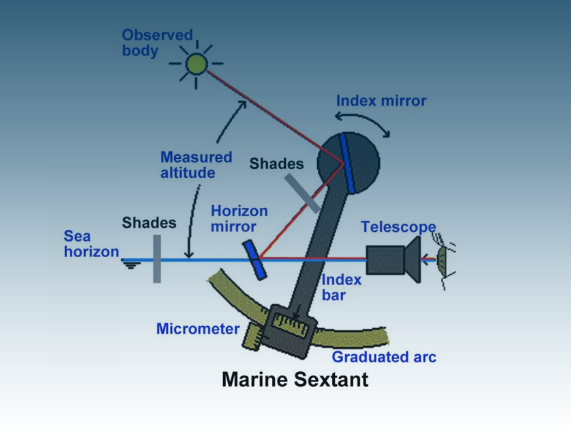
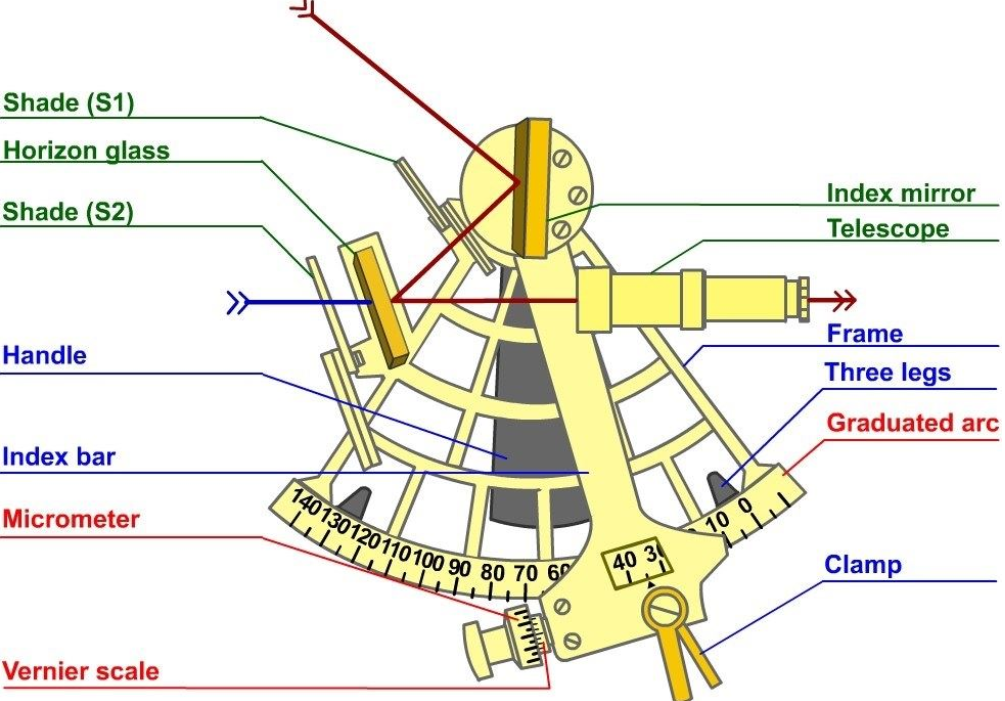
A marine sextant consists of a system of two mirrors and a telescope mounted on a metal frame.

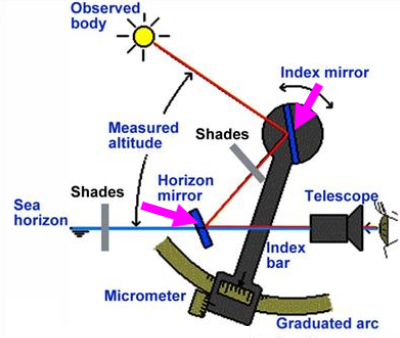
The rigid horizon mirror is a semi translucent mirror attached to the frame.
The shade glasses are used when the object looked at is bright – such as the sun.

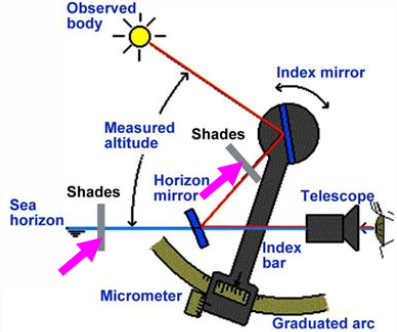
The fully reflecting index mirror is mounted on the index arm rotatable on a pivot perpendicular to the frame.

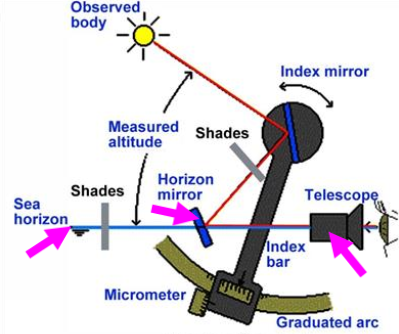
When measuring an altitude, the instrument frame is held in a vertical position and the visible sea horizon is viewed through the telescope and horizon mirror.

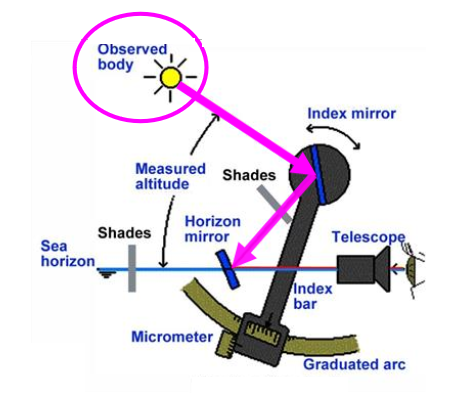
A Light ray coming from the observed body is first reflected by the index mirror and then by the back surface of the horizon mirror before entering the telescope.

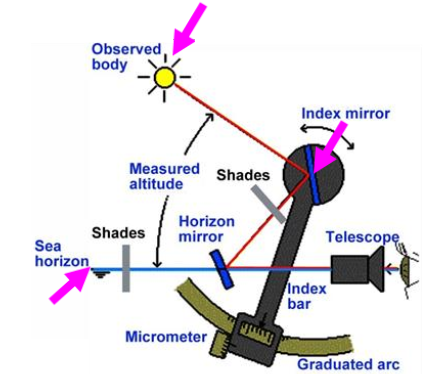
By slowly rotating the index mirror on the pivot the superimposed image of the observed body is aligned with the image of the horizon.

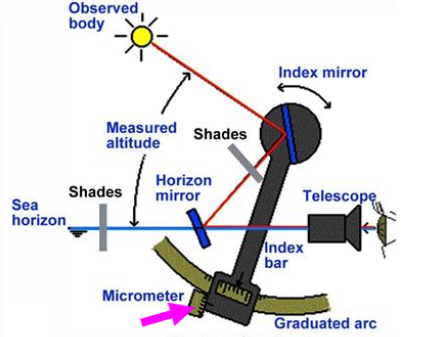
The measured altitude, which is twice the angle formed by the planes of horizon glass and index mirror, can be read from micrometer with Vernier scale from the graduated arc.

A marine sextant is a high – precision optical instrument.

To achieve this precision, a sextant is built from high precision mechanical parts made from a special temperature compensating alloy.

The instrument should be handled with adequate care which is also the reason why sextants are normally kept in quality wooden boxes.

Working Principle of Sextant

The sextant basically consist of a telescope, a half- silvered horizon mirror which the telescope “looks” through and a moving index bar on which the index mirror is fixed.

BY manipulating this index bar, observed body ( a star or other celestial body) can be made to appear on the horizon.
Accurate adjustments are made by means of a micrometer knob.

The angle can then be read off the graduated arc and micrometer.

The principle of sextant is:

⦁ When a ray of light is reflected by a plane mirror, the angle of the incident ray is equal to the angle of the reflected ray, when the incident ray, reflected ray and the normal lie on the same plane.
⦁ When a ray of light suffers two successive reflections in the same plane by two plane mirrors, the angle between the incident ray and the reflected ray is twice the angle between the mirrors.

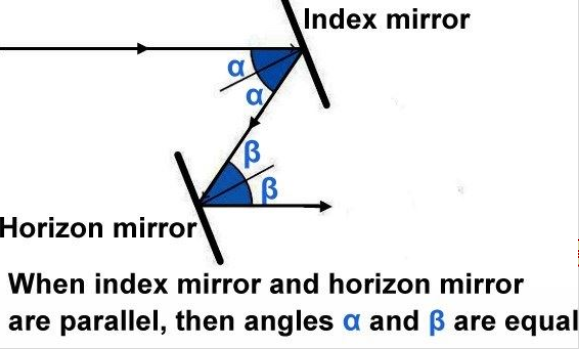
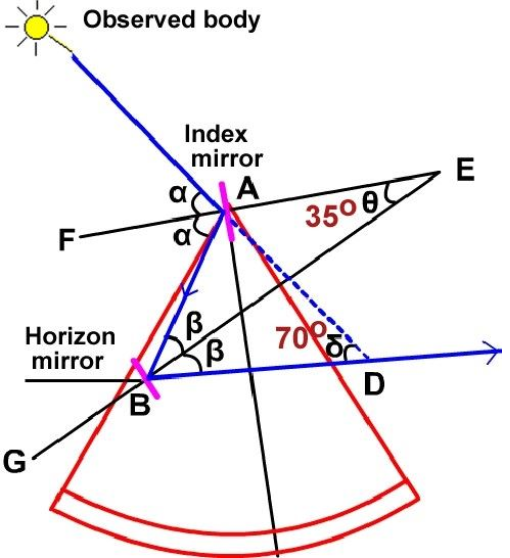
Double reflectivity depends upon the principle that the angle of incidence of a ray α of light equals its angle of reflection β when the two mirrors (index and horizon mirrors) are parallel.

When the mirror is rotated away from the parallel, the total change in the angle of reflection from the rotated mirror δ is twice the amount of rotation θ

Example:

If an observer body is 70 degrees above the horizon, the index mirrors must be displaced by 35 degrees in order to send its reflected light rays through the telescope.

Proof:-

Let θ represent the angle between the mirrors.
Let δ represent the angle between the intial and final directions of a ray of light.

The required proof is : δ=2 θ
Angle CAF= angle FAB = α and,
Angle ABE= angle EBD= β

(Angles of incidence and reflection)

In triangle ABD 2α=2β + δ…………(1)
(External angle= sum of internally opposite angles)
In triangle ABE, α= β + θ
(External angle= sum of internally opposite angles)
So, 2α= 2β + 2θ………………….(2)
Equation (1) = Equation (2) as both = 2α
So, 2β+ δ=2β+2θ and hence δ=2θ