What is Celestial Navigation!!!
Celestial navigation includes finding your ships position at sea using various celestial bodies such as the sun, the moon, the planets and the stars. It does not imply navigation among the stars as you probably imagined.
While there are various modem electronic position finding systems provided on the ships now, none of them are fail-safe. Celestial navigation therefore remains the basic and unfailing mode of finding your position when at sea.
To obtain our position on the earth’s surface using celestial bodies, it is necessary to use the data relating to the accurately established Positions of the celestial bodies and to relate this to our position on the earth. Let us now establish the co-ordinates used in defining the position of celestial bodies.
In the concept of celestial navigation, we assume that all the heavenly bodies are plotted on a uniform sphere called the celestial sphere as if they are all at the same distance. (Remember, they are at vast differing distances from each other!) Their Positions on this celestial sphere are carefully calculated so that at any moment we can spot the Celestial body and use it to fix our position.
Definitions
Great circles and small circles
The shape of the earth is an oblate spheroid; i.e. it is flattened at the poles and bulging at the equator. However for most practical purposes of navigation the earth is considered a sphere.
Spherical trigonometry is Concerned with properties of the spherical triangles on the surface of a sphere A great circle is a circle on the surface of a sphere, the plane of which passes through the centre of the sphere. A great circle thus divides a sphere in two equal halves. The earth, being assumed a sphere, the equator and all meridians are great circles.
A small circle is one whose plane does not pass through the centre of the sphere. A parallel of latitude is thus a small circle by definition. The pole of a great circle is that point on the surface of the sphere, which is equidistant from all points on that circle. All great circles have two poles.
The celestial sphere
This is a sphere of infinite radius with its centre at the centre of the earth. All the celestial bodies the sun, the moon, the stars and planets appear projected on the inside of the sphere, irrespective of the distance of the bodies from the earth.
The celestial poles
These are the two points on the celestial sphere, where the axis of the earth (the diameter of the earth about which it rotates.) produced, meets the celestial sphere. Thus, we have the North celestial pole, vertically above the North Pole and the south celestial pole vertically above the South Pole of the Earth.
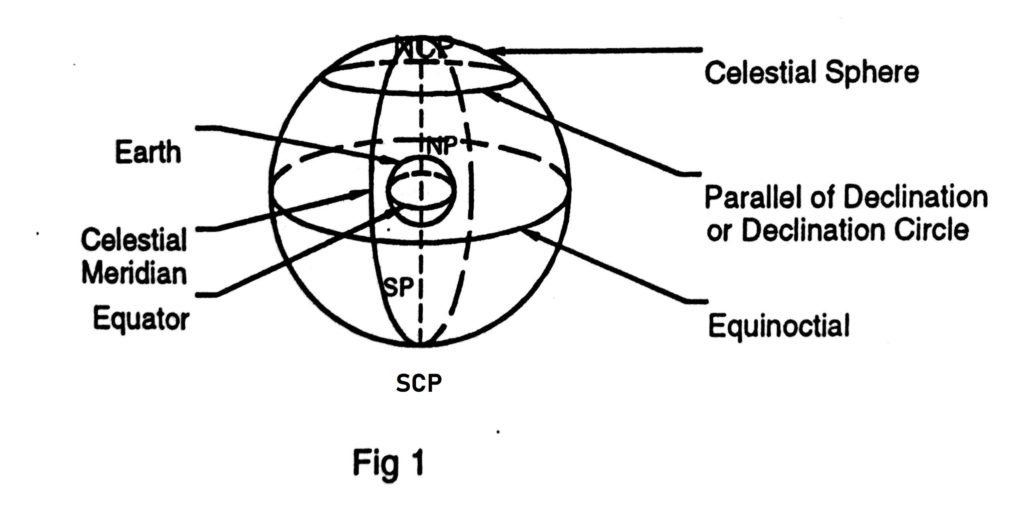
The equinoctial
This Is a great circle on the celestial sphere In the same plane as the plane of the earth’s equator. It we project the Earth’s equator outwards, the circle formed where It moots the celestial sphere would be the equinoctial. Every point on the equinoctial Is 90 degrees from the two celestial poles.
parallels of declination
These are small circles on the celestial sphere, the planes of which are parallel to the plane of the equinoctial. These are similar to parallel of latitudes on the earth.
Celestial Meridians
These are semi-great-circles on the celestial sphere, joining the celestial poles. The other half of the same great circle is another celestial meridian, 1804 away. Celestial meridians intersect the equinoctial and parallels of declination at right angles.
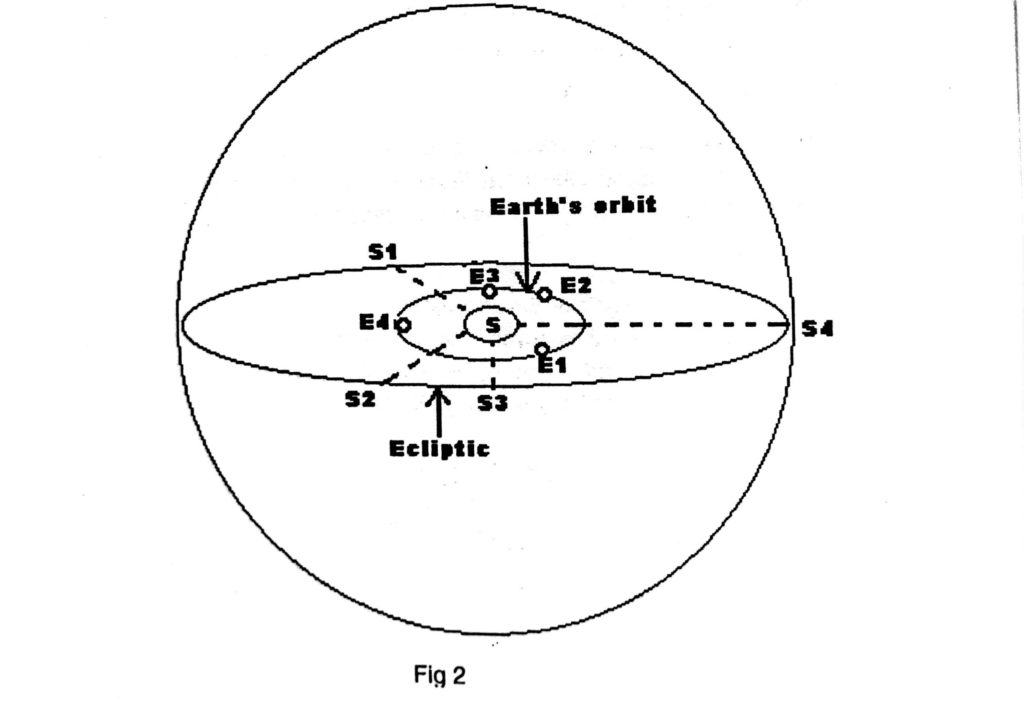
The ecliptic
This is a great circle on the celestial sphere in the same plane as the plane of the Earth’s orbit around the sun. Thus, the ecliptic is the apparent annual path of the Sun on the celestial sphere. When the earth is at E1 in fig 2, the sun appears to be at S1 , on the celestial sphere. As the earth move to E2, E3 and E4 the sun appears to move to S2, S3 and S4 respectively.
This apparent path of the sun on the celestial sphere is a great circle and is called the ecliptic. In other words the elliptical orbit of the earth, around the sun, projected on the celestial sphere forms the ecliptic. The plane of the earth’s orbit around the sun and therefore the plane of the ecliptic is inclined at 23 degrees 26.7- minutes (written as 23° 26.7′) to the plane of the equinoctial. This angle between the planes is known as the obliquity of the ecliptic.
Pole of the Ecliptic
A point 90° removed from any great circle is called its pole. Similarly Ecliptic, being, a great circle, has its own pole, 90° removed from the ecliptic. This point is known as the pole of the ecliptic. This point also does not appear on the earth’s surface, since, ecliptic itself does not appear on the earth.
Any two great circles on a sphere, the planes of which are not the same will intersect each other at two points 180 degrees apart, dividing each of them in two halves.
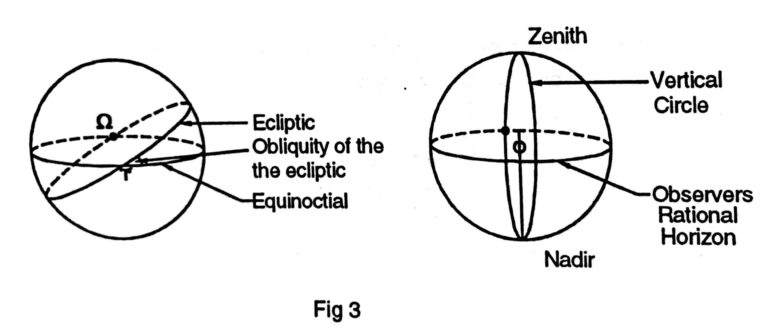
Since the equinoctial and the ecliptic are inclined to each other, they will also intersect each other at points 180 degrees apart. These two points are referred to as the equinoxes. On 21st March, at vernal equinox, the sun on its apparent path along the ecliptic crosses the equinoctial from the south on its northern path. This point is known as the first point of Aries, denoted by the Greek letter ɤ. Similarly on 23rd September at autumnal equinox, the sun appears to cross the equinoctial , from the north to south. This point is known as the first point of Libra, denoted Ω.
The observers' Zenith
This is the point on the celestial sphere vertically above the observer. That is the point at which a straight line from the centre of the earth, through the observer meets the celestial sphere.
The observer's Nadir
This is the point on the celestial sphere, vertically opposite the zenith. The observer’s rational horizon This is a great circle on the celestial sphere, every point on which is 90 degrees away from his zenith.
Vertical Circles
These are great circles on the celestial sphere, passing through the observers’ zenith and the nadir.
The observer's prime vertical
This is the vertical circle passing through the east and west points on his rational horizon.
Celestial co-ordinates
A position on a sphere may be defined by stating the angles at the centre of the sphere or the arcs of great circles contained between that position and two reference great circles, which are at right angles to each other. For example, a position on the earth can be defined by stating such angles or arcs with respect to the two great circles at right angles to each other, viz. the equator from which latitudes are measured and the Greenwich meridian from which longitudes are measured.
Equinoctial
Equinoctial is a great circle, on the celestial sphere in the sameplane as the equator on the earth. In other words, the equator when projected upwards & drawn on the celestial sphere is called the “Equinoctial”.
Celestial pole
Earth’s pole when projected on to the celestial sphere is called the celestial Pole and is 90° removed from the equinoctial; just as the earth’s pole are 90° away from the equator.
Parallels of Declination
Parallels of latitudes on the earth, projected on to the celestial sphere are called parallels of Declination. Declination in the celestial sphere corresponds exactly to latitudes on the earth’s surface, and helps to express the position of a heavenly body, North or South of the Equinoctial
Obliquity of the ecliptic
The angle at which the ecliptic crosses the equinoctial is called the obliquity of the ecliptic. This value is 23° 27′ approximately, and varies very slightly by a few seconds of arc each year on either side of its mean value which is assumed to be constant at 23° 27′ of arc without producing any appreciable error.
The first point of Aries ɤ
This is the imaginary fixed point on the celestial sphere where the ecliptic crosses the equinoctial when the Sun is moving from South to North in Declination.
First point of Libra Ω
This is the point where the Ecliptic crosses the equinoctial when the Sun is moving from North to South Declination. This point is diametrically opposite to first point of Aries. These are also the two fixed points of “Equinoxes”, where the Declination of the Sun is Zero
Celestial Meridians
Any meridian on the earth when projected upwards to the celestial sphere is a celestial meridian. In other words they are half great circles running from celestial pole to pole and crossing the equinoctial at right angles of the infinite number of such meridians, which can be drawn on the celestial sphere, that specific meridian passing through the first point of Aries has a special significance. It is a reference meridian from which the East/ West co-ordinates on the celestial sphere are measured, something similar to the Greenwich (prime) meridian on the earth’s surface from which longitudes east or west is measured.
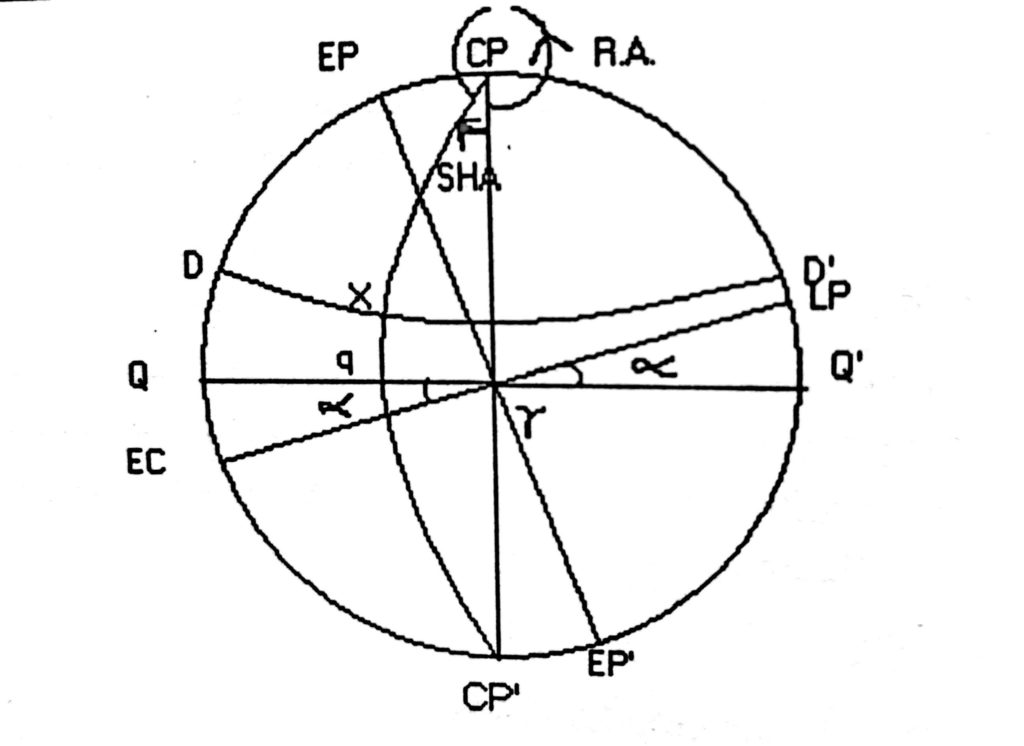
In fig. 4 above
QQ’ is the Equinoctial.
DD’ Is the Parallel of Declination of X
Ec Lp is the Ecliptic
Cp is the Celestial pole
ɤ is the the first point of Aries
Angle = QɤEc = LpɤQ is the Obliquity of the Ecliptic
Cp Cp’ is the Celestial meridian
X is a heavenly body
Arc qX is the Declination of body X
ɤq =Angle ɤCpX is the SHA of body X
Sidereal Hour Angle: (SHA)
Is the angle at the celestial pole or the arc of the equinoctial contained between the meridian of 1st point of Aries and the celestial meridian passing through the heavenly body, always measured westwards and expressed in degrees, minutes and seconds of arc. (Arc ɤq or angle ɤCpq in the fig. 4)
Note that, unlike longitudes on the earth, which are measured both East & West of the prime meridian; SHA is always measured westwards only and will increase from zero degrees to 360°.First point of Aries being a fixed point in space, the Declination and SHA of heavenly body will give the fixed co-ordinates of that body at any time, and these are given in the nautical almanac for all heavenly bodies used for Navigational purposes. Thus by knowing the Declination and SHA of a heavenly body, that body can be pinpointed in the celestial sphere.
Right Ascension
(RA) is the angle at the Celestial pole or the arc of the equinoctial contained between the meridian of 1st point of Aries and the celestial meridian passing through the body, but always measured Eastwards and expressed in hours, minutes and seconds of time (see fig.). Hence SHA + RA in arc = 360° always for any body. For purposes of navigation, however, the term RA is not commonly used.
Celestial Latitudes
These are lines drawn parallel to the ecliptic both north & south of the ecliptic.
Celestial Longitudes
These are similar to celestial meridians but drawn from North ecliptic pole to South ecliptic pole and cross the Ecliptic at Right angles. Both celestial Latitudes & celestial Longitudes are parameters not used for the purposes of Navigation.
2 thoughts on “Celestial Navigation”