After reading this blog, you will be able to take amplitude of the heavenly bodies and calculate the compass error. Ensure that you workout such errors as frequently as possible when on onboard.
Since refraction causes celestial bodies to appear elevated in the sky, they are above the horizon longer than they are otherwise. The mean diameter of sun and moon Is each about 32′.
Let us consider a case when an observer measures the altitude of sun a lower limb when It is just touching the horizon, by a Sextant (I.E = 0) and HE = 0, i.e. his eye is at the water level.
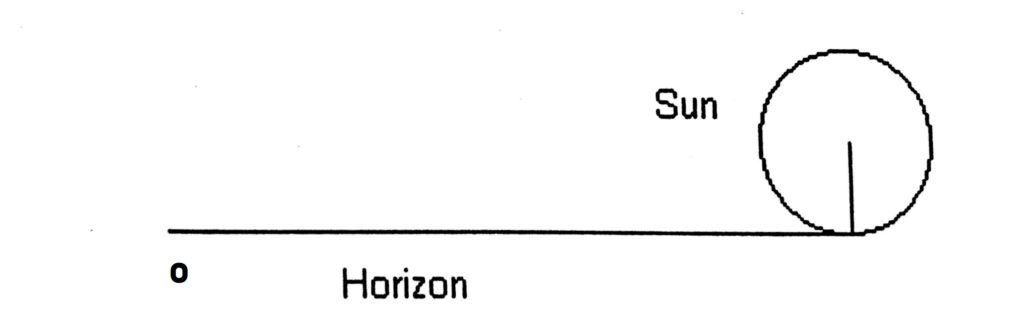
From Diagram It is evident the apparent altitude of the Sun is 0° while the centre of Sun is one Semi-diameter above the horizon. If you glance through ‘Altitude Correction Tables 0° – 10° Sun, Stars, Planets’ you will notice that total correction for apparent altitude of LL. of sun is -18.2′ i.e. the true altitude of suns centre is
Apparent Altitude = 00° 00′
Total Correction = 00° 18.2′
∴ True altitude = — 00° 18.2′
i.e. The True altitude of Suns centre is 18.2′ below the horizon but for the observer the suns centre appears to be about 00°16′ above the horizon.
∴ Cos (90 — Dec) = Cos ∠ Z X Sin (90 — Lat)
∴ Sin (Dec) = Cos ∠ Z X Cos Lat
I.e. Cosine Azimuth = Sin Declination X Secant Latitude
The compass error can be found by comparing the Compass bearing with the calculated Azimuth.
Twilight
The period of daylight for any observer is the interval between sunset and sunrise. When the sun sets below the rational horizon the light is not suddenly cut off. Although the observer does not receive direct sunlight the atmosphere will still be sunlit. Scattering and reflection of suns light by atmosphere allows some light to reach the observer indirectly. The amount of light reaching the observer keeps on decreasing as the sun’s depression below the horizon increases.
The interval between the setting of sun and when very little or no light reaches the observer is called as evening twilight. It is impossible to determine the exact moment when no light reaches the observer. For this reason twilight is considered to end or begin when the sun’s centre is 18° below the rational horizon. This period of twilight is further sub-divided as follows:
Position of centre w.r.t. Rational horizon.
00° – 06° Civil Twilight
06° – 12° Nautical Twilight
12° to 18° Astronomical Twilight
The time of Sunrise, Sunset duration of twilight varies with the latitude of the observer. This information is given for various latitudes between 72° N and 60° S to the nearest whole minute in the nautical almanac.
Finding Time of Sunrise and Sunset (from Nautical Almanac)
Enter the table on the daily page, and extract the LMT for the tabulated latitudes, which lie on either side of the observer’s latitude. Interpolate for the latitude determining the correct LMT. Where necessary apply the correction to obtain the ship’s Zone time.
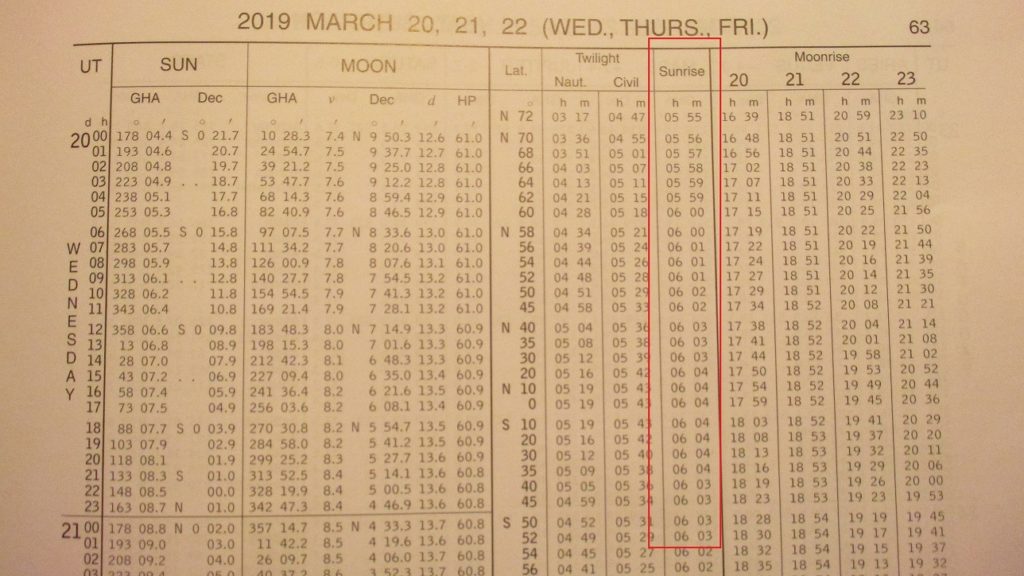
Note: In the Nautical Almanac, Sunrise, Sunset and Twilight Tables are given only once for the middle of the three days on each page. For most purposes this information can be used for all three days.
Finding Time Of Twilight:
The time of Civil and Nautical Twilight is given in the Nautical Almanac.
In general, the most effective period for observing stars and Planets occur when the centre of the Sun is between 3° and 9° below the horizon. It would therefore be prudent to take sight when Sun’s centre is 6° below the horizon i.e. at the end of Civil Twilight.
Determine from the almanac the LMT of twilight (upper part of daily page for morning twilight and lower part of the daily page for morning twilight) for the latitudes tabulated on either side of observer’s latitude. Interpolate and then apply the zone time to determine ships time of twilight.